توزیع نرمال چیست و چه کاربردی دارد؟

توزیع نرمال یکی از بنیادی‌ترین و مهم‌ترین توزیع‌های آماری است که در بسیاری از زمینه‌های علمی و عملی کاربردهای گسترده‌ای دارد. این توزیع، به‌ویژه در آمار و علوم اجتماعی، طبیعی و مهندسی به‌عنوان یک مدل استاندارد، برای توزیع داده‌ها در نظر گرفته می‌شود. توزیع نرمال به‌طور معمول به‌عنوان یک توزیع متقارن و زنگوله‌ای توصیف می‌شود که در آن بیشتر مشاهدات در اطراف میانگین قرار دارند. در توزیع نرمال احتمال بروز مقادیر بسیار بزرگ یا کوچک به تدریج کاهش می‌یابد. این ویژگی سبب می‌شود که توزیع نرمال قادر به مدل‌سازی بسیاری از پدیده‌های طبیعی و انسانی باشد، از جمله قد افراد، نمرات آزمون‌ها، خطاهای اندازه‌گیری و… .

یک ویژگی برجسته‌ی توزیع نرمال، ارتباط آن با قانون حد مرکزی است که بیان می‌کند با افزایش تعداد مشاهدات، توزیع‌های مختلف به‌سوی توزیع نرمال تمایل پیدا می‌کنند. این امر سبب شده است که توزیع نرمال نه‌تنها به‌عنوان یک توزیع تجربی، بلکه به‌عنوان یک ابزار نظری و عملی در آمار و تحلیل داده‌ها مدنظر قرار گیرد. در این متن، به بررسی ویژگی‌ها، اهمیت و کاربردهای توزیع نرمال خواهیم پرداخت و به توضیح نحوه‌ی کاربرد آن در تحلیل‌ داده‌ها و تصمیم‌گیری‌های مبتنی بر شواهد خواهیم رسید.

ریاضی را آنلاین و خصوصی یاد بگیرید!

تاریخچه توزیع نرمال یا گاوسی

ریشه‌های ابتدایی

مفاهیم مربوط به توزیع نرمال به قرن 18 و 19 میلادی برمی‌گردد. در آن زمان، ریاضیدانان به بررسی توزیع‌های آماری و خطاهای محاسباتی پرداختند.

کارهای کارل فردریش گاوس

توزیع نرمال به نام کارل فردریش گاوس، ریاضیدان و ستاره‌شناس آلمانی، نام‌گذاری شده است. او در اوایل قرن 19 میلادی در مطالعه خود درباره خطای اندازه‌گیری، به معرفی و تحلیل این توزیع پرداخت. گاوس نشان داد که خطاهای اندازه‌گیری به‌طور معمول در یک توزیع نرمال قرار می‌گیرند.

پیشرفت توزیع نرمال

در ادامه، دیگر ریاضیدانان و محققان مانند پیتر دی موور و آگوستین لویی کوشی نیز در فهم و توسعه توزیع نرمال نقش داشتند.

قانون حد مرکزی

در اوایل قرن 20 میلادی، مفهوم قانون حد مرکزی به‌طور گسترده‌ای شناخته شد. این قانون بیان می‌کند که مجموع متغیرهای تصادفی مستقل و همگن، حتی اگر توزیع آن‌ها نرمال نباشد، به توزیع نرمال گرایش می‌یابد. این مفهوم تأکید می‌کند که چرا توزیع نرمال در آمار و علوم مختلف تا این حد مهم است.

کاربردها

توزیع نرمال به یکی از ستون‌های اصلی آمار تبدیل شده است و در زمینه‌های مختلفی از جمله روانشناسی، اقتصاد، جامعه‌شناسی و علوم طبیعی کاربرد دارد.توزیع نرمال به دلیل ویژگی‌های خاص خود، مانند اینکه حدود 68% داده‌ها در یک انحراف معیار از میانگین و 95% داده‌ها در دو انحراف معیار قرار دارند، در تحلیل داده‌ها و برآوردهای آماری مورد استفاده قرار می‌گیرد.

مطلب پیشنهادی: ماتریس همانی چیست؟

تعریف توزیع نرمال

توزیع نرمال (Normal Distribution) یکی از مهم‌ترین توزیع‌های احصایی و آماری است که به دلیل ویژگی‌های خاص خود در بسیاری از زمینه‌ها مورد استفاده قرار می‌گیرد. این توزیع به شکل یک منحنی زنگی (Bell Curve) نمایش داده می‌شود . درواقع توزیع نرمال به وضعیتی اشاره دارد که اگر شما یک گروه بزرگ از داده‌ها، مثل نمرات دانش‌آموزان در یک امتحان را جمع‌آوری کنید، این نمرات به شکلی خاص و متقارن پخش می‌شوند.

ویژگی‌های توزیع نرمال

شکل منحنی

توزیع نرمال به صورت متقارن و به شکل زنگی است. این به این معناست که داده‌های نزدیک به میانگین بیشتر از داده‌های دورتر از میانگین هستند. به عنوان مثال اگر نمرات را روی یک نمودار رسم کنید، به شکل یک زنگ است، یعنی بیشتر افراد نمراتی نزدیک به میانگین (میانگین نمرات) کسب می‌کنند و تعداد کمتری نمراتی خیلی بالا یا خیلی پایین دارند.

میانگین، میانه و نما

در توزیع نرمال، سه پارامتر فوق برابر هستند و در مرکز منحنی قرار دارند. برای مثال ، نمرات حول یک مقدار مرکزی (میانگین) پخش می‌شوند. یعنی به طور متوسط اکثر افراد نمراتشان حدوداً به یک اندازه (میانگین) نزدیک است، و تعداد افرادی که نمرات خیلی بالا یا خیلی پایین دارند کمتر است.

استاندارد‌سازی

توزیع نرمال استاندارد (Standard Normal Distribution) با μ = 0 و σ = 1 فرم خاصی از توزیع نرمال است که در آن میانگین برابر صفر و انحراف معیار برابر یک است.

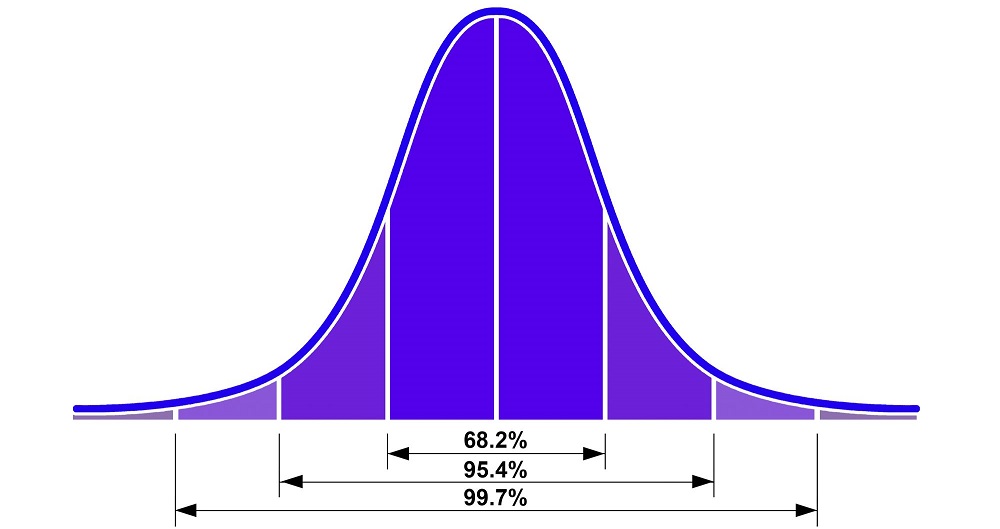
قانون 68-95-99.7

در این توزیع، تقریباً 68% داده‌ها در یک انحراف معیار از میانگین، 95% داده‌ها در دو انحراف معیار و 99.7% داده‌ها در سه انحراف معیار از میانگین قرار دارند.

• تقریباً 68% از افراد نمراتی در حدود یک انحراف معیار ( به معنای فاصله از میانگین) از میانگین دارند.
• تقریباً 95% از افراد نمراتی در حدود دو انحراف معیار از میانگین دارند.
• تقریباً 99.7% از افراد نمراتی در حدود سه انحراف معیار از میانگین دارند.

عدم وجود مقادیر منفی

در توزیع نرمال، احتمال بروز مقادیر بسیار شدید (بسیار مثبت یا منفی) کاهش می‌یابد، بنابراین مقادیر در انتهای توزیع به تدریج کاهش می‌یابند؛ به همین دلیل معمولاً هیچ مقداری به طور قطعی نمی‌تواند صفر یا منفی باشد.

بسیاری از مقادیر طبیعی

بسیاری از پدیده‌های طبیعی، مانند قد، نمرات امتحانی و خطای اندازه‌گیری، به طور تقریبی توزیع نرمال دارند.

پیشنهاد نویسنده: ماتریس چیست؟

کاربرد توزیع نرمال

توزیع نرمال در بسیاری از حوزه‌ها مانند اقتصاد، روانشناسی، علوم اجتماعی، و بسیاری از رشته‌های علمی دیگر کاربرد دارد. به عنوان مثال، آن می‌تواند برای مدل‌سازی نتایج آزمون‌ها، اندازه‌گیری خطاها و تجزیه و تحلیل داده‌ها استفاده شود. توزیع نرمال ابزار بسیار مفیدی است زیرا می‌توانیم با استفاده از آن پیش‌بینی کنیم که در یک گروه بزرگ، چه درصدی از افراد نمرات نزدیک به میانگین، متوسط یا خیلی پایین یا خیلی بالا خواهند داشت. توزیع نرمال را می توانید در نرم افزار SPSS و سایر نرم افزار های آماری به دست بیاورید.

آموزش آنلاین نرم افزار SPSS

مثال برای توزیع نرمال

برای درک بهتر بیایید با مثالی بهتر با توزیع نرمال آشنا شویم. این مثال نشان می‌دهد که چطور توزیع نرمال می‌تواند به ما در درک و تجزیه و تحلیل داده‌ها کمک کند.

نمرات امتحان

فرض کنید یک کلاس شامل 100 دانش‌آموز وجود دارد که در یک امتحان ریاضی شرکت کرده‌اند. نمرات این دانش‌آموزان به صورت زیر توزیع شده است:

• میانگیین نمرات 75 از 100
• انحراف معیار 10

نمرات نزدیک به میانگین

بر اساس ویژگی‌های توزیع نرمال، اکثر دانش‌آموزان نمراتی نزدیک به 75 خواهند داشت. به طور خاص، تقریباً 68% از دانش‌آموزان، نمراتی بین 65 (75 – 10) و 85 (75 + 10) خواهند داشت. یعنی 68 نفر از 100 دانش‌آموز نمراتشان در این بازه خواهد بود.

نمرات بالاتر و پایین‌تر

تقریباً 95% دانش‌آموزان نمراتی در بازه 55 (75 – 20) تا 95 (75 + 20) خواهند داشت. یعنی حدود 95 نفر از 100 دانش‌آموز نمراتشان میان این دو عدد خواهد بود. در نهایت، تقریباً 99.7% از دانش‌آموزان نمراتی بین 45 (75 – 30) و 105 (75 + 30) خواهند داشت. در واقع، تعداد خیلی کمی از دانش‌آموزان نمرات خارج از این محدوده خواهند داشت .

تصویر کلی

با توجه به این توزیع، می‌توانیم بگوییم که اکثر دانش‌آموزان نمرات متوسط و بالا خواهند داشت و تنها تعداد کمی از دانش‌آموزان نمرات خیلی پایین یا خیلی بالا خواهند داشت.

مطلب پیشنهادی: تحلیل سری زمانی چیست؟

اهمیت توزیع نرمال

توزیع نرمال (Normal Distribution) اهمیت های زیادی دارد که به شرح زیر است:

مدل‌سازی بسیاری از پدیده‌ها

توزیع نرمال به‌خوبی می‌تواند بسیاری از پدیده‌های طبیعی و اجتماعی را مدل‌سازی کند. برای مثال، توزیع قد افراد، نمرات امتحانی و خطاهای اندازه‌گیری غالباً به توزیع نرمال نزدیک هستند.

استفاده در آمار استنباطی

بسیاری از آزمون‌های آماری، مانند t-test و ANOVA، فرض می‌کنند که داده‌ها از توزیع نرمال تبعیت می‌کنند. این آزمون‌ها به محققان این امکان را می‌دهند که به‌طور صحیح نتایج را تجزیه و تحلیل و تفسیر کنند.

فرمایش مرکزی

بر اساس نظریه‌ی حد مرکزی (Central Limit Theorem)، مجموع یا میانگین متغیرهای تصادفی مستقل که هر یک دارای توزیع مشابهی باشند به توزیع نرمال تمایل پیدا می‌کند. این تمایل بدون توجه به توزیع اولیه آن‌ها می باشد. این اصل به محققان این امکان را می‌دهد که در بسیاری از موارد حتی زمانی که توزیع اولیه نرمال نیست، از توزیع نرمال به عنوان یک تقریب استفاده کنند.

 تسهیل در محاسبات

توزیع نرمال دارای خواص ریاضی مطلوبی است که انجام محاسبات مربوط به احتمال و آمار را ساده می‌کند. این به محققان و تحلیل‌گران کمک می‌کند تا محاسبات پیچیده را به راحتی انجام دهند.

مدل‌سازی خطی

– در مدل‌های رگرسیون خطی، فرض بر این است که خطاها از توزیع نرمال پیروی می‌کنند. این فرض به تحلیل‌گران این امکان را می‌دهد که نتایج تحلیل‌های رگرسیونی را به درستی تفسیر کنند.

مدیریت ریسک

در حوزه‌های مالی مانند ترید و بورس و اقتصادی، توزیع نرمال به‌عنوان یک مدل بنیادی برای تجزیه و تحلیل و مدیریت ریسک استفاده می‌شود. بسیاری از ریسک‌هایی که در بازارهای مالی وجود دارند، می‌توانند به‌طور تقریباً نرمال توزیع شوند.

تفسیر نتایج

ویژگی‌های آسان توزیع نرمال (همچون درصدها و درصدهای معین محصور شده در انحراف استانداردها) به محققان کمک می‌کند تا نتایج خود را به راحتی تفسیر کنند و با اطمینان بیشتری به تصمیم‌گیری بپردازند.

مطلب پیشنهادی: نحوه خواندن ریاضی برای کنکور

توزیع نرمال و فرمول آن، سفری به دنیای اعداد

حال بیایید نگاهی عمیق‌تر به این مفهوم بیندازیم و فرمول آن را بررسی کنیم.

فرمول توزیع نرمال

تابع چگالی احتمال توزیع نرمال (Normal Distribution) به‌صورت زیر نمایان می‌شود:

در این فرمول:

• ( x): متغیری که می‌خواهید احتمال آن را محاسبه کنید.
• (μ): میانگین جمعیت که مرکز توزیع را مشخص می‌کند.
• (σ): انحراف استاندارد که میزان پراکندگی داده‌ها را حول میانگین نشان می‌دهد.
• (e): عدد نپر حدود 2.71828که در ماتریس‌های مختلف ریاضی پایه بسیار مهم است.
• (π): عدد پی حدود 3.14159 که در هندسه و تحلیل‌های ریاضی کاربرد زیادی دارد.

جذابیت توزیع نرمال

حالا که با فرمول آشنا شدیم، این سوال مطرح می‌شود که چرا این توزیع این‌قدر جذاب است؟

توازن طبیعی

توزیع نرمال به‌صورت یک منحنی زنگوله‌ای شکل است که نشان‌دهنده توازن در داده‌هاست. این خاصیت باعث شده که بسیاری از پدیده‌های طبیعی به این توزیع نزدیک شوند.

کشف قوانین جهان

در علم، بسیاری از قوانین اساسی، از جمله قوانین فیزیک و روانشناسی، بر مبنای توزیع نرمال تعریف می‌شوند. به عنوان مثال، در علوم اجتماعی و انسانی، بسیاری از متغیرها مانند استعدادها و رفتارها به‌طور تقریباً نرمال توزیع می‌شوند.

نظریه حد مرکزی

یکی از جذاب‌ترین ویژگی‌های توزیع نرمال، نظریه حد مرکزی است. این نظریه بیان می‌کند حتی اگر متغیرهای اولیه به خودی خود توزیع نرمال نداشته باشند، میانگین یا مجموع آنها در نهایت به توزیع نرمال نزدیک می‌شود. این ویژگی باعث می‌شود که توزیع نرمال در بسیاری از تحلیل‌ها اهمیت پیدا کند.

پس توزیع نرمال نمایانگر زیبایی و نظم در دنیای اعداد است. این فرمول ساده، که در عین حال پیچیدگی‌های زیادی را در خود نهفته دارد، به ما این امکان را می‌دهد که با دقت و اطمینان تجزیه و تحلیل کنیم. با کاوش بیشتر در این موضوع، می‌توانید به درکی عمیق‌تر از چگونگی تأثیر الگوها و توزیع‌ها بر دنیای واقعی دست یابید.

مطلب پیشنهادی: الگوریتم فیبوناچی چیست؟

مقاله مربوط به توزیع نرمال

اگر به دنبال مقالات علمی یا منابع آموزشی بیشتر هستید، می‌توانید به مقالات مرتبط با توزیع نرمال در نشریات آمار و تحلیل داده، مانند  Journal of the American Statistical Association یا  American Statistical Association  مراجعه کنید. این منابع می‌توانند شما را در درک عمیق‌تر و کاربردهای متنوع توزیع نرمال یاری کنند.

چرا به توزیع نرمال، نرمال میگویند؟

توزیع نرمال به دلیل ویژگی‌های خاصی که دارد، “نرمال” نامیده می‌شود. در واقع این توزیع به‌طور گسترده‌ای در طبیعت و در توزیع‌های آماری داده‌ها مشاهده می‌شود. پیشینه استفاده از این اصطلاح به قرن نوزدهم برمی‌گردد و به شایع بودن و معمول بودن خاصیت‌های آن در داده‌های مختلف اشاره دارد. از جمله دلایل اینکه توزیع نرمال “نرمال” نامیده می‌شود می‌توان به موارد زیر اشاره کرد:

شکل زنگوله‌ای

توزیع نرمال دارای شکل خاص و متقارن، شبیه به زنگوله است که بسیاری از پدیده‌های طبیعی و انسانی را به خوبی مدل می‌کند. می‌گیرد که امکان پیش‌بینی و تحلیل بهتر داده‌ها را فراهم می‌کند.

قانون حد مرکزی

این توزیع به‌عنوان نتیجه‌ای از قانون حد مرکزی شناخته می‌شود، که بیان می‌کند اگر تعداد زیادی از متغیرهای تصادفی مستقل با توزیع یکسان جمع شوند، توزیع مجموع آنها تقریباً نرمال خواهد بود.

موارد کاربردی فراوان

توزیع نرمال در بسیاری از زمینه‌ها مانند علم، مهندسی، اقتصاد و علوم اجتماعی به‌طور گسترده‌ای مورد استفاده قرار می‌گیرد. به همین دلیل، آن را “نرمال” می‌نامند. به این ترتیب، توزیع نرمال به دلیل ویژگی‌های منحصر به فرد و کاربردهای فراوانش به‌عنوان یک توزیع “نرمال” در دنیای علم و آمار شناخته می‌شود. از توزیع نرمال در الگوریتم های بسیار زیادی از جمله الگوریتم مارکوف استفاده می شود.

پیشنهاد نویسنده: تحلیل سری زمانی چیست؟

مواردی که از توزیع نرمال پیگیری میکنند

قد افراد

قد انسان‌ها معمولاً توزیع نرمالی دارد، به‌طوری که بیشتر افراد دارای قد نزدیک به میانگین و تعداد کمتری افراد با قدهای بسیار بلند یا کوتاه وجود دارد.

نمرات آزمون‌ها

نمرات در آزمون‌های استاندارد مانند SAT و GRE، معمولاً توزیع نرمالی را نشان می‌دهند.

خطاهای اندازه‌گیری

در بسیاری از آزمایش‌های علمی و صنعتی، خطاهای طبیعی در اندازه‌گیری‌ها به‌طور تصادفی و نرمال توزیع می‌شوند.

ویژگی‌های اقتصادی

برخی از ویژگی‌های اقتصادی مانند درآمد خانوار، در بعضی از جوامع به‌طور تقریباً نرمال توزیع می‌شود.

زمان‌های پردازش

در زمینه‌های محاسباتی و تولیدی، زمان‌های پردازش وظایف و کارها معمولاً توزیع نرمال دارند.

فشار خون

فشار خون افراد در یک جمعیت به‌صورت نرمال توزیع می‌شود، که این امر باعث می‌شود به راحتی بتوان حداکثر و حداقل نرمال را تعیین کرد.

توزیع خطا در مدل‌های پیش‌بینی

در مدل‌سازی‌های رگرسیونی، معمولاً فرض می‌شود که خطاها به‌صورت نرمال توزیع شده‌اند.

موجودات زنده

برخی از صفات بیولوژیکی مانند وزن، دامنه بینایی و صفات دیگر موجودات زنده معمولاً به‌طور نزدیک به نرمال توزیع می‌شوند. این موضوعات به‌ویژه در علم آمار و روش‌های تحلیلی اهمیت زیادی دارند، زیرا بسیاری از آزمون‌ها و تکنیک‌های آماری بر پایه فرض نرمال بودن داده‌ها بنا شده‌اند.

مطلب پیشنهادی: تراز چیست؟ چه تفاوتی با رتبه دارد؟

محدودیت های توزیع نرمال

توزیع نرمال ویژگی‌ها و کاربردهای زیادی دارد، اما همچنین محدودیت‌هایی نیز دارد با آگاهی از این محدودیت‌ها، محققان و تحلیل‌گران می‌توانند انتخاب‌های بهتری در استفاده از توزیع‌ها و تکنیک‌های آماری انجام دهند.در ادامه به برخی از آن‌ها اشاره می‌شود:

• توزیع غیرنرمال داده‌ها: بسیاری از داده‌ها به طور طبیعی توزیع نرمال ندارند. به عنوان مثال، توزیع‌های مقیاس‌پذیر، چپ‌برگردان، یا ارزش‌های خارج از محدوده (outliers) می‌توانند به وضوح نامتقارن باشند و از توزیع نرمال پیروی نکنند.
• عدم تطابق در داده‌های پایین یا بالا: توزیع نرمال فرض می‌کند که داده‌ها از میانگین به طور متقارن پراکنده شده‌اند. در صورتی که داده‌ها متقارن نباشند یا دارای دم‌های سنگین (heavy tails) باشند، استفاده از توزیع نرمال می‌تواند منجر به تخمین‌های نادرست شود.
• حساسیت به اندازه نمونه: توزیع نرمال فقط در جمع‌آوری داده‌ها و نمونه‌های بزرگ قابل اعتبار است. در نمونه‌های کوچک، حتی اگر داده‌ها از توزیع نرمال تبعیت کنند، نتایج آماری ممکن است به‌طور قابل توجهی متفاوت از آنچه انتظار می‌رود باشند.
• عدم وجود تابع چگالی برای برخی کاربردها: در برخی موارد، استفاده از توزیع نرمال برای مدل‌سازی شرایط واقعی مناسب نیست. مثلاً در مواردی که مقادیر مرزی وجود دارد، مثلاً زمانی که مقادیر نمی‌توانند کمتر از صفر باشند، توزیع‌های نرمال مناسب نیستند.
• کاهش اطلاعات: فرضیات توزیع نرمال، مانند میانگین و انحراف معیار، اطلاعات زیادی را در خود دارند. این ممکن است منجر به از دست دادن اطلاعاتی درباره توزیع واقعی داده‌ها شود.
• محدودیت در پیش‌بینی نوسانات: توزیع نرمال برای برخی از پدیده‌ها که دارای نوسانات شدید یا ناگهانی هستند مانند بازارهای مالی مناسب نیست و اغلب این نوسانات با توزیع‌های دیگر مانند توزیع‌های نرمال متاخر یا توزیع‌های پارتو مدل‌سازی می‌شوند.

سخن نهایی

توزیع نرمال یکی از مهمترین توزیع هایی است که بشر برای اندازه گیری آمار های مختلف در حال حاضر از آن استفاده می کند. البته که در شروع این توزیع به این صورت که ما هم اکنون می شناسیم نبوده و با پیشرفت علم آمار و ریاضیات اندکس های مختلفی به ان اضافه شده است. در این محتوا سعی کردیم شما را با مفهوم کلی توزیع نرمال و البته تاریخچه این اندکس آماری آشنا کنیم. امیدواریم این مطلب برای شما مفید بوده باشد. حتما نظرات خودتان را برای ما بنویسید.