ماتریس اسکالر چیست؟

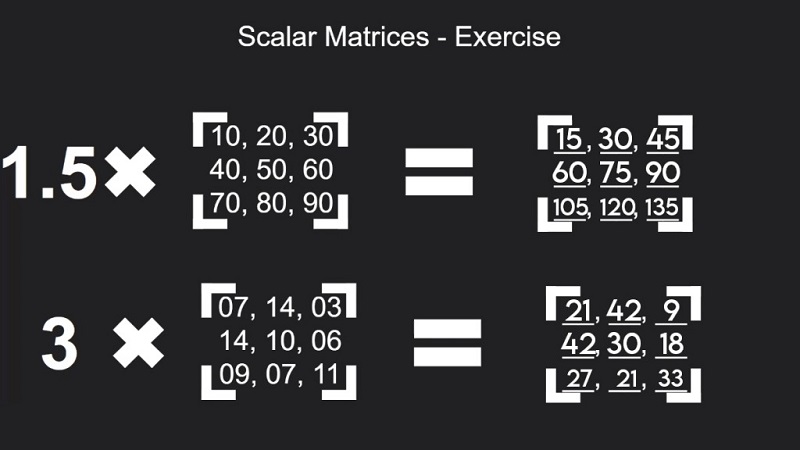
در جبر خطی، ماتریس یکی از مفاهیم بنیادی است که برای نمایش و تحلیل داده‌های ساختار یافته به کار می‌رود. ماتریس‌ها به طور گسترده‌ای در علوم مختلف از جمله ریاضیات، آموزش فیزیک، مهندسی و اقتصاد کاربرد دارند. یکی از انواع خاص ، ماتریس اسکالر است که به دلیل ویژگی‌های خاص خود، در بسیاری از محاسبات نقش مهمی ایفا می‌کند. در این مقاله، به بررسی جامع و تخصصی ماتریس‌های اسکالر می‌پردازیم و ویژگی‌ها، خواص و کاربردهای آن‌ها را مورد مطالعه قرار می‌دهیم.

آموزش تخصصی ریاضی با بهترین اساتید ایران

تعریف ماتریس اسکالر

ماتریس اسکالر، یک ماتریس مربعی است که تمام درایه‌های قطر اصلی آن با هم برابرند و درایه‌های خارج از قطر اصلی، همگی صفر هستند. به عبارت دیگر، اگر k یک عدد اسکالر و I ماتریس واحد باشد، ماتریس A یک ماتریس اسکالر است اگر و تنها اگر A = kI باشد.

به صورت ریاضی، یک ماتریس اسکالر n × n به شکل زیر نمایش داده می‌شود:

A =

| k 0 0 … 0 |

| 0 k 0 … 0 |

| 0 0 k … 0 |

| . . . . . |

| 0 0 0 … k |

در این مثال ، k یک عدد اسکالر دلخواه و تمام درایه‌های خارج از قطر اصلی برابر با صفر هستند.

مطلب پیشنهادی: چرا ریاضی رو یاد نمیگیرم؟

ویژگی‌های ماتریس اسکالر

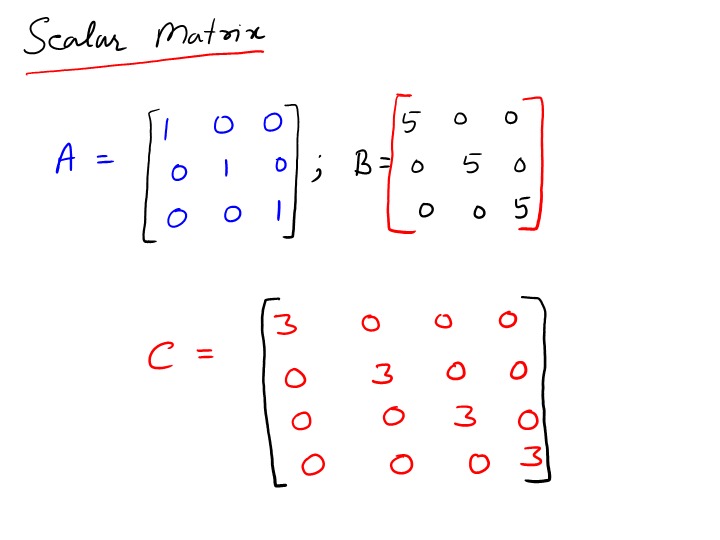
• قطری بودن: همواره قطری هستند.
• تغییرناپذیری در ضرب ماتریسی: ضرب یک ماتریس اسکالر در هر ماتریس دیگر، معادل ضرب تمام درایه‌های آن ماتریس در اسکالر مربوطه است. به عبارت دیگر، اگر A یک ماتریس اسکالر و B یک ماتریس دلخواه باشد، آنگاه AB = BA = kB.
• همانی ضرب: ماتریس واحد یک ماتریس اسکالر خاص است که در آن k = 1 می‌باشد.
• ماتریس صفر: ماتریس صفر نیز یک ماتریس اسکالر است که در آن k = 0 می‌باشد.

خواص ماتریس اسکالر

• جمع ماتریس‌های اسکالر: جمع دو ماتریس اسکالر نیز یک ماتریس اسکالر است.
• ضرب اسکالر در اسکالر: ضرب یک اسکالر در یک ماتریس اسکالر، یک ماتریس اسکالر جدید تولید می‌کند.
• معکوس ماتریس اسکالر: هر ماتریس اسکالر غیرصفر دارای معکوس است و معکوس آن نیز یک ماتریس اسکالر است.

کاربردهای ماتریس اسکالر

ماتریس‌های اسکالر در بسیاری از محاسبات ماتریسی کاربرد دارند، از جمله:

• تغییر اندازه ماتریس‌ها: ضرب یک ماتریس در یک ماتریس اسکالر، باعث تغییر اندازه تمام درایه‌های آن ماتریس می‌شود.
• تعریف ضرب داخلی: در برخی فضاهای برداری، ضرب داخلی دو بردار به صورت ضرب ماتریسی یک بردار در ترانهاده بردار دیگر تعریف می‌شود. در این حالت، استفاده از ماتریس‌های اسکالر می‌تواند برای تعریف ضرب داخلی‌های مختلف مفید باشد.
• حل دستگاه معادلات خطی: ماتریس‌های اسکالر در روش‌های عددی حل دستگاه معادلات خطی کاربرد دارند.
• تبدیلات خطی: ماتریس‌های اسکالر می‌توانند برای نمایش تبدیلات خطی از قبیل مقیاس‌بندی (scaling) استفاده شوند.

مطلب پیشنهادی: نحوه خواندن ریاضی برای امتحان نهایی

روش‌های محاسباتی با ماتریس‌های اسکالر

همانطور که در بخش‌های قبلی دیدیم، ماتریس‌های اسکالر به دلیل ساختار ساده و ویژگی‌های منحصربه‌فرد خود، در محاسبات ماتریسی نقش مهمی ایفا می‌کنند. در این بخش، به بررسی دقیق‌تر روش‌های محاسباتی با ماتریس‌های اسکالر و کاربردهای آن‌ها در حل مسائل مختلف می‌پردازیم.

عملیات پایه با ماتریس‌های اسکالر

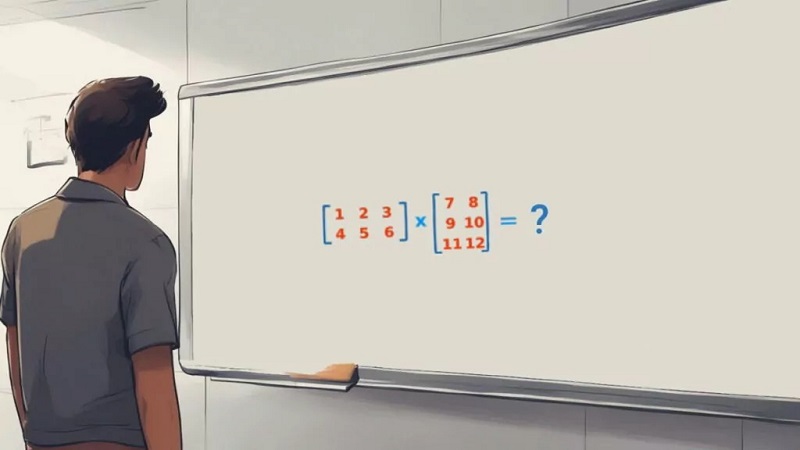
• جمع و تفریق: جمع و تفریق ماتریس‌های اسکالر به سادگی با جمع یا تفریق درایه‌های متناظر آن‌ها انجام می‌شود.
• ضرب ماتریسی: ضرب یک ماتریس اسکالر در یک ماتریس دلخواه به این صورت انجام می‌شود که هر درایه از ماتریس دلخواه در اسکالر مربوطه ضرب می‌شود.

کاربردهای محاسباتی ماتریس‌های اسکالر

• تغییر اندازه ماتریس‌ها: یکی از مهم‌ترین کاربردهای ماتریس‌های اسکالر، تغییر اندازه ماتریس‌ها است. با ضرب یک ماتریس در یک ماتریس اسکالر، می‌توان تمام درایه‌های آن ماتریس را بزرگ‌تر یا کوچکتر کرد.
• مقیاس‌بندی بردارها: در هندسه تحلیلی، می‌توان از ماتریس‌های اسکالر برای مقیاس‌بندی بردارها استفاده کرد.
• تنش و کرنش: در مکانیک جامدات، ماتریس‌های اسکالر برای نمایش تنش‌های یکنواخت و کرنش‌های یکنواخت استفاده می‌شوند.

مطلب پیشنهادی: نحوه تست زنی برای کنکور

روش‌های عددی با ماتریس‌های اسکالر

• روش‌های تکراری: در روش‌های تکراری حل دستگاه معادلات خطی، از ماتریس‌های اسکالر برای ایجاد ماتریس‌های پیش شرطی استفاده می‌شود. این ماتریس‌ها سرعت همگرایی روش‌های تکراری را بهبود می‌بخشند.
• روش‌های تجزیه ماتریسی: در روش‌های تجزیه ماتریسی مانند روش LU و QR، ماتریس‌های اسکالر می‌توانند برای ساده‌سازی محاسبات استفاده شوند.

پیاده‌سازی ماتریس‌های اسکالر در نرم‌افزارهای ریاضی

پس از بررسی مفاهیم نظری و محاسباتی ماتریس‌های اسکالر، به سراغ پیاده‌سازی عملی این مفهوم در نرم‌افزارهای ریاضی می‌رویم. نرم‌افزارهای ریاضی به دلیل قابلیت‌های قدرتمند خود در انجام محاسبات ماتریسی، ابزار مناسبی برای کار با ماتریس‌های اسکالر هستند. در این بخش، به بررسی نحوه پیاده‌سازی ماتریس‌های اسکالر در برخی از پرکاربردترین نرم‌افزارهای ریاضی می‌پردازیم.

پیاده‌سازی در نرم‌افزار MATLAB

MATLAB یکی از قدرتمندترین نرم‌افزارهای محاسبات عددی است که به طور گسترده‌ای در مهندسی و علوم استفاده می‌شود. در MATLAB، ماتریس‌های اسکالر به سادگی با استفاده از دستور eye ایجاد می‌شوند. این دستور یک ماتریس واحد ایجاد می‌کند که با ضرب در یک اسکالر، به ماتریس اسکالر تبدیل می‌شود.

پیاده‌سازی در نرم‌افزار Python با کتابخانه NumPy

NumPy یک کتابخانه قدرتمند در زبان برنامه‌نویسی پایتون است که برای انجام محاسبات عددی به کار می‌رود. در NumPy، ماتریس‌ها به صورت آرایه‌های چندبعدی نمایش داده می‌شوند. برای ایجاد یک ماتریس اسکالر، می‌توان از تابع np.eye استفاده کرد و سپس آن را در یک اسکالر ضرب کرد.

مطلب پیشنهادی: نحوه خواندن ریاضی برای کنکور

پیاده‌سازی در نرم‌افزار Mathematica

Mathematica یک نرم‌افزار ریاضی قدرتمند است که برای انجام محاسبات نمادین و عددی به کار می‌رود. در Mathematica، ماتریس‌های اسکالر به سادگی با استفاده از تابع IdentityMatrix ایجاد می‌شوند.

پیاده‌سازی در نرم‌افزار Maple

Maple یک نرم‌افزار ریاضی قدرتمند است که برای انجام محاسبات نمادین و عددی به کار می‌رود. در Maple، ماتریس‌های اسکالر به سادگی با استفاده از تابع Matrix ایجاد می‌شوند.

کاربردهای پیاده‌سازی ماتریس‌های اسکالر در نرم‌افزارها

• حل دستگاه معادلات خطی: ماتریس‌های اسکالر در روش‌های تکراری حل دستگاه معادلات خطی به کار می‌روند.
• شبیه‌سازی سیستم‌های دینامیکی: ماتریس‌های اسکالر در مدل‌سازی و شبیه‌سازی سیستم‌های دینامیکی کاربرد دارند.
• پردازش تصویر: ماتریس‌های اسکالر در پردازش تصویر برای تغییر روشنایی و کنتراست تصاویر استفاده می‌شوند.
• یادگیری ماشین: ماتریس‌های اسکالر در طراحی الگوریتم‌ های یادگیری ماشین برای تنظیم پارامترها استفاده می‌شوند.

مطلب پیشنهادی: صف در ساختمان داده چیست؟

ماتریس‌های اسکالر در مکانیک کوانتومی: یک نگاه عمیق

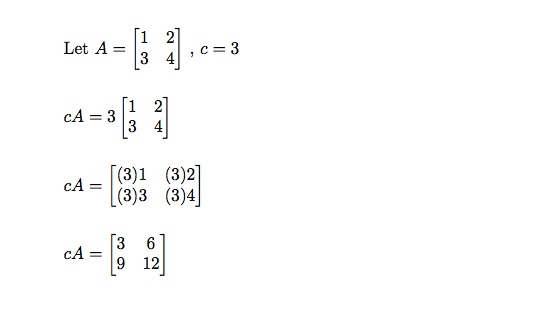
مکانیک کوانتومی، شاخه‌ای از فیزیک است که به مطالعه رفتار ماده در مقیاس اتمی و زیر اتمی می‌پردازد. در این تئوری، بسیاری از کمیت‌های فیزیکی مانند انرژی، تکانه و اسپین با عملگرهای خطی نمایش داده می‌شوند که می‌توان آن‌ها را به صورت ماتریس نشان داد. ماتریس‌های اسکالر، به عنوان یک نوع خاص از ماتریس‌ها، نقش مهمی در توصیف برخی از پدیده‌های کوانتومی ایفا می‌کنند. در این بخش، به بررسی نقش ماتریس‌های اسکالر در مکانیک کوانتومی می‌پردازیم.

ماتریس‌های اسکالر و عملگرهای همانی

یکی از مهم‌ترین کاربردهای ماتریس‌های اسکالر در مکانیک کوانتومی، نمایش عملگر همانی (Identity operator) است. عملگر همانی، عملگری است که هر حالت کوانتومی را به خودش نگاشت می‌کند. در نمایش ماتریسی، عملگر همانی به صورت یک ماتریس اسکالر با درایه‌های قطر اصلی برابر با 1 نمایش داده می‌شود.

ماتریس‌های اسکالر و مقیاس‌بندی حالت‌های کوانتومی

ماتریس‌های اسکالر همچنین می‌توانند برای مقیاس‌بندی حالت‌های کوانتومی استفاده شوند. ضرب یک حالت کوانتومی (که به صورت یک بردار نمایش داده می‌شود) در یک ماتریس اسکالر، باعث می‌شود که دامنه (amplitude) همه اجزای آن بردار به یک اندازه تغییر کند. این عمل، در واقع تغییر در احتمال یافتن ذره در حالت‌های مختلف است.

مطلب پیشنهادی: پردازش داده چیست؟

ماتریس‌های اسکالر و فضاهای هیلبرت

در مکانیک کوانتومی، حالت‌های کوانتومی به عنوان بردارهایی در یک فضای هیلبرت نمایش داده می‌شوند. فضای هیلبرت، یک فضای برداری با بعد نامتناهی است که در آن ضرب داخلی تعریف شده است. ماتریس‌های اسکالر در تعریف ضرب داخلی در فضای هیلبرت نقش مهمی ایفا می‌کنند.

ماتریس‌های اسکالر و نظریه اختلال

در نظریه اختلال، که برای محاسبه تقریبی مقادیر ویژه و بردارهای ویژه یک عملگر استفاده می‌شود، ماتریس‌های اسکالر نقش مهمی دارند. در این نظریه، اغلب از ماتریس‌های اسکالر برای نمایش اختلالات کوچک در سیستم استفاده می‌شود.

مطلب پیشنهادی: رسم نمودار سه بعدی در متلب

سخن نهایی

در این مقاله، به بررسی جامع ماتریس‌های اسکالر پرداخته شد. از تعریف پایه و ویژگی‌های این نوع خاص از ماتریس‌ها آغاز کرده و به کاربردهای گسترده آن‌ها در زمینه‌های مختلف از جمله جبر خطی، محاسبات عددی، مکانیک کوانتومی و پیاده‌سازی در نرم‌افزارهای ریاضی پرداختیم. ماتریس‌های اسکالر به دلیل سادگی ساختار و ویژگی‌های خاص خود، ابزاری قدرتمند در تحلیل و حل مسائل مختلف هستند. با درک عمیق از این مفهوم، می‌توان از آن برای مدل‌سازی پدیده‌های پیچیده، انجام محاسبات عددی دقیق و پیاده‌سازی الگوریتم‌های مختلف استفاده کرد. از جمله مهم‌ترین کاربردهای ماتریس‌های اسکالر می‌توان به تغییر اندازه ماتریس‌ها، مقیاس‌بندی بردارها، تعریف ضرب داخلی، حل دستگاه معادلات خطی، تبدیلات خطی و نمایش عملگر همانی در مکانیک کوانتومی اشاره کرد. همچنین، پیاده‌سازی آسان این ماتریس‌ها در نرم‌افزارهای ریاضی مانند MATLAB، Python، Mathematica و Maple، امکان استفاده گسترده از آن‌ها را در تحقیقات و کاربردهای مختلف فراهم می‌کند. در پایان، می‌توان گفت که ماتریس‌های اسکالر، به عنوان یک مفهوم بنیادی در جبر خطی، نقشی کلیدی در پیشرفت علوم و مهندسی ایفا می‌کنند.